Botte, Marko
Hotz, T., Huckemann, S., Le, H., Marron, J. S., Mattingly, J. C., Miller, E., Nolen, J., Owen, M., Patrangenaru, V., Skwerer, S. (2013). Sticky central limit theorems on open books. Annals of Applied Probability, 23(6) 2238-2258 , 1202.4267
Huckemann, S. (2011). Intrinsic Inference on the Mean Geodesic of Planar Shapes and Tree Discrimination by Leaf Growth Ann. Statist., 39 (2), 1098–1124, arXiv 1009.3203
Huckemann, S., Hotz, T., Munk, A. (2010). Intrinsic shape analysis: Geodesic principal component analysis for Riemannian manifolds modulo Lie group actions. Discussion paper with rejoinder. Statistica Sinica, 20. pp. 1-100
Huckemann, S., Hotz, T., Munk, A. (2010). Intrinsic MANOVA for Riemannian Manifolds with an Application to Kendalls Spaces of Planar Shapes. IEEE Trans. Patt. Anal. Mach. Intell., 32 (4). pp. 593-603. "Spotlight Paper" for this issue with its "Special Section on Shape Analysis and its Applications in Image Understanding"
In the contemporary sciences, many challenges lead to data that lie on high dimensional spaces often featuring curvature and singularities. The sphere or the hyperbolic disk are but simple examples of such non-Euclidean spaces. For data on these spaces, already elementary statistical methods cannot be applied. For instance, classically a mean is the sum of data points divided by their number. But how to add points on a sphere and divide them by a number?
In Statistics on non-Euclidean Spaces we design new statistical methodology for such spaces, such as geodesic PCA and more generally (semi)-intrinsic statistical analysis involving data descriptors on stratified spaces. It turns out that such descriptors often feature new non-Euclidean limiting laws, opening a wide field of Mathematical Statistics yet to explore. Methods derived are applied to existing challenges in the fields of:
Early stem cell differentiation
Fingerprint analysis
Gait analysis of knee joint
Growth analysis of forest-biometrical objects
Modelling and statistics of body organ shapes
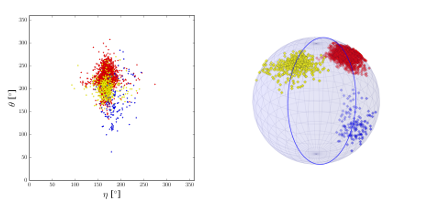
Three clusters of different RNA backbone geometries. They overlap in the classic pseudo-torsion representation (left) but can easily be separated using non-Euclidean statistical methods (right).