Dick, J., Rudolf, D., Zhu, H. (2016). Discrepancy bounds for uniformly ergodic Markov chain quasi-Monte Carlo. Annals of Applied Probability. 26 (2016), pp. 3178 - 3205
Rudolf, D., Sprungk, B. (2016). On a generalizition of the preconditional Crank-Nicolson Metropolis algorithm. Found. Comput. Math. (accepted)
Latuszynski, K., Rudolf, D. (2015). Convergence of hybrid slice sampling via spectral gap. https://arxiv.org/abs/1409.2709 (submitted)
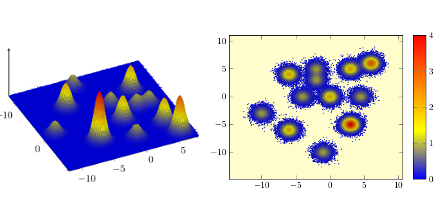
Markov chain Monte Carlo methods, in particular Metropolis-Hastings type algorithms, are one of the key tools in computational statistics for the approximation of distributions and expected values. For inference in Bayesian statistics as well as in the area of uncertainty quantification it is desirable to sample according to partially known posterior distributions. In high dimensions this can be very challenging, in particular, for multi-modal distributions. The left figure illustrates a multi-modal mixture of 12-Gaussian distributions. The right figure contains 105 sample points generated with a hybrid slice sampling Markov chain. Here all modes are discovered.
We develop and investigate methods which are robust with respect to the dimension, especially, in such complex settings. Our focus is on hybrid slice sampling, Metropolis-type algorithms as well as quasi-Monte Carlo methods. In the analysis of difficult data sets also approximating, cheaper versions of Markov chain algorithms are promising alternatives.